Fibonacci sayısı oluşturma - Matematik Problemi

Fibonacci sayılarını oluşturmanın birden fazla yöntemi vardır.

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 141, ……..

Fn = Fn-1 + Fn-2

F0 = 0 and F1 = 1.

Metot 1 ( recursion )

Yukarıda verilmiş olan matematik ifadesinin direkt olarak uygulanmış halidir. İşe yarar ama çok fazla maliyetlidir.

T(n) = T(n-1) + T(n-2) karmaşıklık analizi çözüldüğünde karşımıza O(2^n) çıkar. Gerçekten maliyetli bir çözüm!

def recursion(n):
    if n <= 1:
        return n
    return recursion(n - 1) + recursion(n - 2)

if __name__ == '__main__':
    n = 9
    print(recursion(n))

Metot 2 (Dynamic Programming)

Metot 1'deki öz yinelemeli çözümde aynı değerleri defalarca hesapladıımızı görmüşsünüzdür. Bu işlemi önlemek amaçlı dinamik programlama yaklaşımına bakacağız.

def dynamic(n):
    fib_list = [0, 1]
    for i in range(2, n + 1):
        fib_list.append(fib_list[i - 1] + fib_list[i - 2])
    return fib_list[n]

if __name__ == '__main__':
    n = 9
    print(dynamic(n))

Bu çözümün zaman karmaşıklığı O(n) ve yer karmaşıklığı O(n) olmaktadır.

Metot 3 (Metot 2 için yer düzenlemesi)

Metot 2'de yapılan çözüm yer karmaşıklığına sahiptir. Yani ekstra bellek kullanımı gerektiren bir çözümdür. Bu çözümü aynı proramlama paradigması ile yerden ödün vermeyerek şu şekilde çözebiliriz.

def space_dynamic(n):
    a, b = 0, 1
    if n == 0:
        return a
    for i in range(2, n + 1):
        a, b = b, a + b
    return b

if __name__ == '__main__':
    n = 9
    print(space_dynamic(n))

Metot 4

Bir başka O(n) çözüme sahip bir çözüm olan bu çözümde elimizde bir matris var.

M = [[1,1],[1,0]]

n. fibonacci sayısını istiyorsak bu matrisi kendisi ile n kere çarpmamız ve (0,0) elemanını almamız gerekmektedir. Kısacası pow(M,n) işlemi yapmamız gerekmektedir.

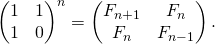
Matris

def matrix(n):
    F = [[1, 1], [1, 0]]
    if not n:
        return 0
    power(F, n - 1)
    return F[0][0]


def power(F, n):
    M = [[1, 1], [1, 0]]
    for i in range(2, n + 1):
        multiply(F, M)


def multiply(F, M):
    x = F[0][0] * M[0][0] + F[0][1] * M[1][0]
    y = F[0][0] * M[0][1] + F[0][1] * M[1][1]
    z = F[1][0] * M[0][0] + F[1][1] * M[1][0]
    w = F[1][0] * M[0][1] + F[1][1] * M[1][1]

    F[0][0] = x
    F[0][1] = y
    F[1][0] = z
    F[1][1] = w

if __name__ == '__main__':
    n = 9
    print(matrix(n))

Zaman karmaşıklığı O(n) ve yer karmaşıklığı O(1) olur.

Metot 5 (Metot 4 iyileştirmesi)

Bu adım ile artık n. fibonacci sayısını bulma işlemini O(logn) karmaşıklıkta çözebileceğiz.

def matrix_opt(n):
    F = [[1, 1], [1, 0]]
    if not n:
        return 0
    power(F, n - 1)
    return F[0][0]


def power_opt(F, n):
    if n == 0 and n == 1:
        return
    M = [[1, 1], [1, 0]]
    power_opt(F, n / 2)
    multiply(F, F)
    if n % 2 != 0:
        multiply(F, M)


def multiply(F, M):
    x = F[0][0] * M[0][0] + F[0][1] * M[1][0]
    y = F[0][0] * M[0][1] + F[0][1] * M[1][1]
    z = F[1][0] * M[0][0] + F[1][1] * M[1][0]
    w = F[1][0] * M[0][1] + F[1][1] * M[1][1]

    F[0][0] = x
    F[0][1] = y
    F[1][0] = z
    F[1][1] = w

if __name__ == '__main__':
    n = 9
    print(matrix_opt(n))

Comments

comments powered by Disqus